Mathematical Logic

Logical Equivalence

Definition 12.20

Any two compound statements A and B are said to be logically equivalent or simply equivalent if the columns corresponding to A and B in the truth table have identical truth values. The logical equivalence of the statements A and B is denoted by A ≡ B or A ⇔ B .

From the definition, it is clear that, if A and B are logically equivalent, then A ⇔ B must be tautology.

 

Some Laws of Equivalence

 

1. Idempotent Laws

(i) p ∨ p ≡ p

(ii) p ∧ p ≡ p .

Proof

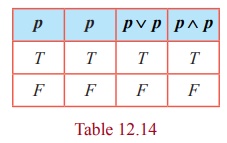
In the above truth table for both p , p ∨ p and p ∧ p have the same truth values. Hence p ∨ p ≡ p and p ∧ p ≡ p .

 

2. Commutative Laws

(i) p ∨ q ≡ q ∨ p

(ii) p ∧ q ≡ q ∧ p .

Proof (i)

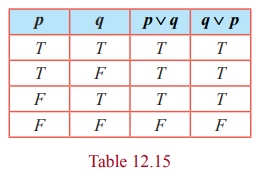
The columns corresponding to p ∨ q and q ∨ p are identical. Hence p ∨ q ≡ q ∨ p .

Similarly (ii) p ∧ q ≡ q ∧ p can be proved.

 

3. Associative Laws

(i) p ∨ ( q ∨ r ) ≡ ( p ∨ q ) ∨ r (ii) p ∧ ( q ∧ r ) ≡ ( p ∧ q ) ∧ r .

Proof

The truth table required for proving the associative law is given below.

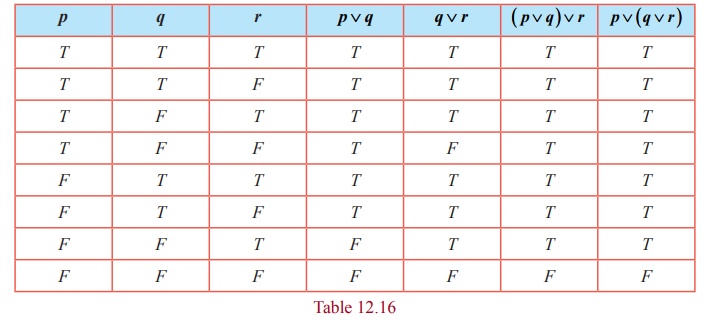
The columns corresponding to ( p ∨ q ) ∨ r and p ∨ ( q ∨ r ) are identical.

Hence p ∨ ( q ∨ r ) ≡ ( p ∨ q ) ∨ r .

Similarly, (ii) p ∧ ( q ∧ r ) ≡ ( p ∧ q ) ∧ r can be proved.

 

4. Distributive Laws

(i) p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r)

(ii) p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r)

Proof (i)

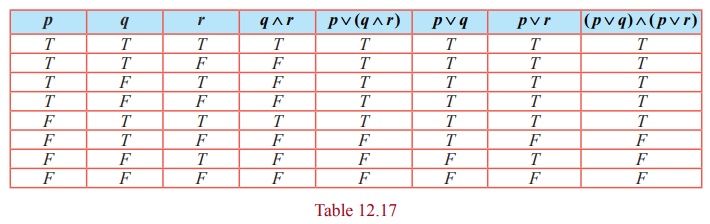
The columns corresponding to p ∨ ( q ∧ r) and ( p ∨ q ) ∧ ( p ∨ r) are identical. Hence p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r) .

Similarly (ii) p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r) can be proved.

 

5. Identity Laws

(i) p ∨ T ≡ T and p ∨ F ≡ p

(ii) p ∧ T ≡ p and p ∧ F ≡ F

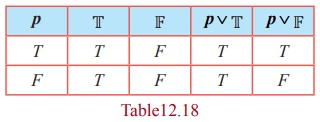
(i) The entries in the columns corresponding to p ∨ T and T are identical and hence they are equivalent. The entries in the columns corresponding to p ∨ F and p are identical and hence they are equivalent.

Dually

(ii) p ∧ T ≡ p and p ∧ F ≡ F can be proved.

 

6. Complement Laws

(i) p ∨ ¬ p ≡ T and p ∧ ¬ p ≡ F (ii) ¬T ≡ F and ¬F ≡ T

Proof

(i) The entries in the columns corresponding to p ∨ ¬ p and T are identical and hence they are equivalent. The entries in the columns corresponding to p ∧ ¬ p and F are identical and hence they are equivalent.

(ii) The entries in the columns corresponding to ¬T and F are identical and hence they are equivalent. The entries in the columns corresponding to ¬F and T are identical and hence they are equivalent.

 

7. Involution Law or Double Negation Law

 ¬(¬ p) ≡ p

Proof

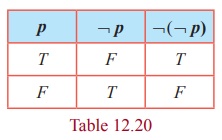
The entries in the columns corresponding to ¬ ( ¬p) and p are identical and hence they are equivalent.

 

8. de Morgan’s Laws

(i) ¬ ( p ∧ q) ≡ ¬ p ∨ ¬q

(ii) ¬ ( p ∨ q) ≡ ¬p ∧ ¬q

Proof of (i)

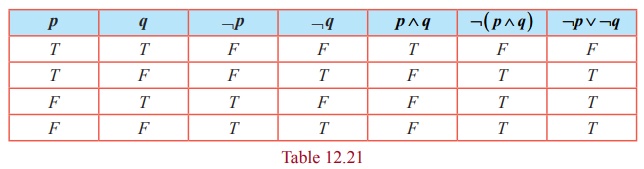
The entries in the columns corresponding to ¬ ( p ∧ q ) and ¬ p ∨ ¬q are identical and hence they are equivalent. Therefore ¬ ( p ∧ q) ≡ ¬ p ∨ ¬q . Dually (ii) ¬ ( p ∨ q) ≡ ¬p ∧ ¬q can be proved.

 

9. Absorption Laws

(i) p ∨ ( p ∧ q ) ≡ p

(ii) p ∧ ( p ∨ q ) ≡ p

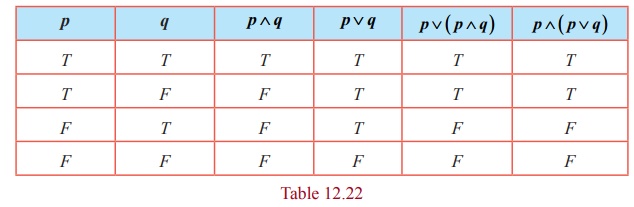
(i) The entries in the columns corresponding to p ∨ ( p ∧ q) and p are identical and hence they are equivalent.

(ii) The entries in the columns corresponding to p ∧ ( p ∨ q) and p are identical and hence they are equivalent.

 

Example 12.17

Establish the equivalence property: p → q ≡ ¬ p ∨ q

Solution

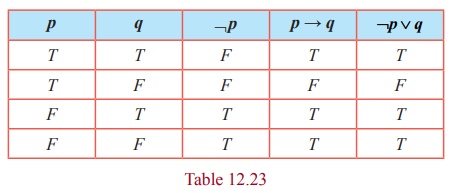
The entries in the columns corresponding to p → q and ¬ p ∨ q are identical and hence they are equivalent.

 

Example 12.18

Establish the equivalence property connecting the bi-conditional with conditional:

 p↔ q ≡ ( p → q ) ∧ (q → p)

Solution

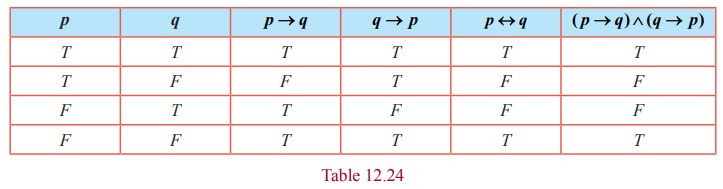
The entries in the columns corresponding to p ↔ q and ( p → q ) ∧ ( q → p) are identical and hence they are equivalent.

 

Example 12.19

Using the equivalence property, show that p ↔ q ≡ ( p ∧ q ) ∨ ( ¬ p ∧ ¬q) .

Solution

It can be obtained by using examples 12.15 and 12.16 that

 p ↔ q ≡ ( ¬ p ∨ q) ∧ ( ¬q ∨ p)

... (1)

≡ (¬ p ∨ q) ∧ ( p ¬q) (by Commutative Law)

... (2)

≡  ( ¬ p ∧ ( p ∨ ¬q )) ∨ ( q ∧ ( p ∨ ¬q)) (by Distributive Law)

≡  ( ¬ p ∧ p) ∨ ( ¬p ∧ ¬q) ∨ ( q ∧ p) ∨ ( q ∧ ¬q) (by Distributive Law)

≡ F ∨ ( ¬p ∧ ¬q) ∨ ( q ∧ p) ∨ F; (by Complement Law)

≡  ( ¬ p ∧ ¬ q ) ∨ ( q ∧ p) ; (by Identity Law)

≡  ( p ∧ q ) ∨(¬ p ¬q) ; (by Commutative Law)

Finally (1) becomes p ↔ q ≡ ( p ∧ q ) ∨(¬ p ¬q) .